Ein paar Anmerkungen zum mathematischen Beweis und zur vollständigen Induktion.
Auf den Gödelschen Unvollständigkeitssatz werde ich hier nicht eingehen, obwohl es einer der wichtigsten Sätze der modernen Logik ist und mir darüber hinaus auch sehr gut gefällt, dass ich nicht ableitbar bin.
Nach der Wikipedia ist ein Beweis:
Ein Beweis ist in der Mathematik die als fehlerfrei anerkannte Herleitung der Richtigkeit bzw. der Unrichtigkeit einer Aussage aus einer Menge von Axiomen, die als wahr vorausgesetzt werden, und anderen Aussagen, die bereits bewiesen sind.
Die Peano-Axiome (auch Dedekind–Peano-Axiome oder Peano-Postulate) sind fünf Axiome, welche die natürlichen Zahlen und ihre Eigenschaften charakterisieren.
Aus der Wikipedia:





Das letzte Axiom heißt Induktionsaxiom, da auf ihm die Beweismethode der vollständigen Induktion beruht. Es ist äquivalent zur Aussage, dass jede Menge natürlicher Zahlen ein kleinstes Element hat. Auch garantiert es, dass Peanos rekursive Definitionen der Addition und Multiplikation auf überhaupt wohldefiniert sind:[3]
überhaupt wohldefiniert sind:[3]




Die Eins definierte Peano als Nachfolger der Null:[4]

Ein Satz oder Theorem ist in der Mathematik eine widerspruchsfreie logische Aussage, die mittels eines Beweises als wahr erkannt, das heißt, aus Axiomen und bereits bekannten Sätzen hergeleitet werden kann.
Ein Satz wird nach seiner Rolle, seiner Bedeutung oder seinem Kontext oft auch anders bezeichnet:
Ein Lemma ist eine Aussage, die als Hilfssatz nur im Beweis anderer Sätze verwendet wird.
Ein Korollar ist eine triviale Folgerung, die sich aus einem Satz oder einer Definition ohne großen Aufwand ergibt.
Der Satz im engeren Sinn gibt eine wesentliche Erkenntnis wieder.
Als Deduktion (deducere – ableiten, weiterführen) bezeichnet man die Folgerung einer besonderen Aussage aus einer allgemeinen. Die Deduktion liefert stets wahre Aussagen.
Jeder Autofahrer hat einen Führerschein. (allgemeine Aussage)
Hansi fährt mit dem Auto.
Hansi hat einen Führerschein. (besondere Aussage)
Als Induktion (inducere – einführen) bezeichnet man den das Erschließen einer allgemeinen Aussage aus Einzelaussagen. Die Induktion kann zu wahren oder falschen Aussagen führen. Es muss jeder Einzelfall auf Wahrheitswert überprüft werden, oder es wird ein Beweis geführt, um die Richtigkeit der Schlussfolgerung festzustellen.
Die vollständige Induktion
gründet sich auf das Induktionsaxiom (siehe oben):
Jede Teilmenge X der Menge der natürlichen Zahlen, die die Zahl 1 und mit jeder Zahl n stets ihren Nachfolger n +1 enthält, ist die Menge der natürlichen Zahlen.
1) 1 ∈ X
2) ∀n∈N:n∈X⇒(n+1)∈X
Daraus folgt X=N
Beweisverfahren der vollständigen Induktion:
Beispiel: ermitteln Sie die Summer der ersten n ungeraden natürlichen Zahlen!
A1: s1 = 1 …… = 1 = 1²
A2: s2 = 1 +3 … = 4 = 2²
A3: s3 = 1 +3 +5 = 9 = 3²
Es ergibt sich die Vermutung, dass sich für jedes n ∈ N eine wahre Aussage ergibt, für folgende Aussageform:
A(n):sn = 1+3+5+…+(2n-1) = n²
Die Vermutung kann durch Einsetzen der natürlichen Zahlen nur für endlich viele natürlich Zahlen bestätigt werden.
Zum Beweis der Algemeingültigkeit von A(n) verwendet man daher das Induktionsaxiom:
1) Induktionsanfang; die Variable n in A(n) wird mit 1 belegt, wodurch der Nachweis erbracht wird, dass A(1) eine wahre Aussage ist.
2) Schluss von n auf n+1; denn A(n+1) ist eine wahre Aussage, wenn A(n) eine wahre Aussage ist.
Induktionsvoraussetzung: A(n): sn = 1+3+5..+(2n-1)=n²
Behauptung: A(n+1): sn+1 = 1+3+5…+(2n-1) +(2n +1) = (n+1)²
Beweis: A(n+1): sn+1 = sn + (2n+1) = n² + (2n+1) = (n+1)²
Die vollständige Induktion ist somit ein deduktives Verfahren unter Zuhilfenahme des Induktionsaxoms.
Beispiele:
- Beweise durch vollständige Induktion: ∀n∈N: 1 + 2 + 3 + . . . + n = 1/2 n (n+1)
- Beweise durch vollständige Induktion, dass 2 hoch n > n ist, für alle n ∈ N
- Ermittle durch vollständige Induktion die Summe wn der Innenwinkel eines konvexen n-Eckes.
- Untersuche, für welche n∈N die ‚Aussageform A(n): n²>2n+1 wahr ist.
- Untersuche, für welche natürliche Zahlen die Aussageform wahr ist: A(n): 2 hoch > n²
- Beweise durch vollständige Induktion, dass für jedes n ∈ N gilt: 1 + 4 + 7 + …+ (3n -2) = 1/2n (3n -1)
- Beweise durch vollständige Induktion, dass für jedes n ∈ N gilt: 1 + 5 + 8 + … + (4n -3) = n(2n-1)
- Beweise durch vollständige Induktion, dass für jedes n ∈ N gilt: 1 + 3 + 6 + 10 + … + 1/2 n (n + 1 ) = 1/6 n(n + 1) (n + 2 )
- Beweise durch vollständige Induktion, dass für jedes n ∈ N gilt: 1.2 + 2.3 + 3.4 + … + n(n + 1) = 1/3 n (n+ 1) (n + 2)
Lösungen finden sich im Kommentarbereich.
Weblinks:
Beweistheorie
* Beweisverfahren der Mathematik
* Beweistraining (pdf) Mit dem Beweis, dass Frauen böse sind. 😉
Satz


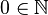




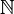 überhaupt
überhaupt