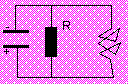zurück zu Kapitel 1
Ich möchte nun auf das Beispiel, welches unter „elektrotonisches Potential“ gegeben wurde, zurückkommen. Man nehme an, dass die zwei Pole des Elko‘s mit einem sehr kleinen R (entspricht einer hohen g Na+) verbunden werden. Elko wird sich schlagartig völlig entladen. Das an der Membran natürlich sehr viel kompliziertere Verhältnisse vorliegen, ist wohl jedem klar, aber trotzdem sind Modelle und Vereinfachungen gefragt, um die wesentlichen Mechanismen in ihrem Prinzip annähernd erfassen zu können. Bei einem AP finden wir nun was bei einer Kondenstorentladung nicht möglich ist – einen overshoot.
Ich erweitere daher das Kondensatormodell um eine Spule und finde somit ein Schwingkreismodell vor. Als Grundlage dafür sehe ich die elektrotonische Ausbreitung der Ionen entlang der Membran (Überwindung des Längswiderstandes; current sink – current source Modell).
Die Ionenbewegung entlang der Membran kann man als Schleife betrachten, die der zum Elko hinzukommenden Spule entspricht.
Bekanntlich kann in einem Schwingkreis die Ladung von der Kondensatorplatte A (nach Anstoß – EPSC) zu B fließen. Dabei wird über die Spule ein elektrisches Feld aufgebaut, welches dem Strom entgegenwirkt. Ohne einen Widerstand (was weder theoretisch noch praktisch möglich ist) käme es zu einer vollständigen Ladungsumkehr, d.h. der Potentialgradient würde nun in die gegensätzliche Richtung weisen. Da aber auch über die Membran ein Widerstand vorhanden ist, kommt es dort eben nur zum overshoot.